Nilai X Yang Memenuhi Persamaan

Dalam matematika, persamaan adalah pernyataan yang menyatakan kesetaraan antara dua ekspresi. Persamaan dapat terdiri dari variabel dan konstanta, dan tujuan kita adalah mencari nilai-nilai dari variabel yang memenuhi persamaan tersebut.

3 Nilai X Yang Memenuhi Persamaan

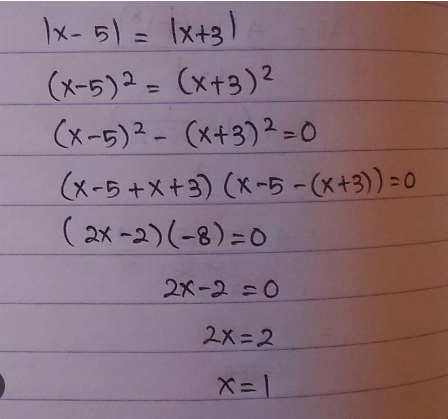
Dalam artikel ini, kita akan membahas bagaimana menemukan nilai X yang memenuhi suatu persamaan:

Untuk memahami konsep ini, mari kita ambil contoh persamaan sederhana: 2X + 5 = 15. Dalam persamaan ini, kita ingin mencari nilai X yang menyebabkan persamaan tersebut menjadi benar. Untuk melakukannya, kita perlu memanipulasi persamaan tersebut dengan menggunakan operasi matematika yang sah.

Langkah pertama yang dapat kita lakukan adalah mengurangi 5 dari kedua sisi persamaan, sehingga persamaan menjadi 2X = 10. Kemudian, kita dapat membagi kedua sisi dengan 2, yang menghasilkan X = 5. Oleh karena itu, nilai X yang memenuhi persamaan tersebut adalah 5.

Namun, tidak semua persamaan begitu sederhana seperti contoh di atas. Dalam beberapa kasus, kita mungkin perlu menerapkan metode atau rumus yang lebih kompleks untuk menemukan nilai-nilai X yang memenuhi persamaan. Berikut adalah beberapa metode yang sering menggunakan:

Metode Substitusi: Metode ini melibatkan menggantikan variabel dengan ekspresi lain dalam persamaan. Misalnya, jika kita memiliki persamaan X^2 – 4X + 3 = 0, kita dapat menggantikan X^2 dengan Y, sehingga persamaan menjadi Y – 4X + 3 = 0. Dengan menggunakan metode ini, kita dapat menemukan nilai-nilai X yang memenuhi persamaan.
Metode Faktorisasi: Metode ini melibatkan mencari faktor-faktor dari ekspresi dalam persamaan dan mengatur persamaan menjadi bentuk perkalian faktor-faktor tersebut. Misalnya, jika kita memiliki persamaan X^2 – 5X + 6 = 0, kita dapat memfaktorkan persamaan menjadi (X – 2)(X – 3) = 0. Dalam hal ini, nilai-nilai X yang memenuhi persamaan adalah 2 dan 3.
Metode Kuadratik: Metode ini menggunakan untuk menyelesaikan persamaan kuadratik, yang memiliki bentuk umum Ax^2 + Bx + C = 0, dengan A, B, dan C sebagai konstanta. Rumus kuadratik yang umum menggunakan adalah X = (-B ± √(B^2 – 4AC)) / (2A). Dengan menggunakan rumus ini, kita dapat menemukan nilai-nilai X yang memenuhi persamaan kuadratik.

Selain metode-metode di atas, ada juga berbagai metode numerik yang dapat menggunakan untuk menemukan nilai-nilai X yang memenuhi persamaan. Metode seperti metode iterasi, metode Newton-Raphson, dan metode biseksi adalah contoh dari metode numerik yang sering menggunakan dalam perhitungan yang lebih kompleks.

Metode Iterasi: Metode ini melibatkan menggunakan pendekatan berulang untuk mendekati nilai-nilai X yang memenuhi persamaan. memulai dengan tebakan awal, kita menerapkan rumus atau algoritma yang menghasilkan nilai baru untuk X. Langkah ini mengulang berulang kali hingga kita mendapatkan pendekatan yang cukup akurat. Metode iterasi berguna ketika tidak ada rumus tertutup yang mengenal untuk menyelesaikan persamaan tersebut.
Metode Newton-Raphson: Metode ini menggunakan untuk menemukan akar persamaan non-linier. Melibatkan aproksimasi iteratif, metode Newton-Raphson memanfaatkan turunan dari persamaan untuk memperbaiki perkiraan awal nilai X. Metode ini efektif untuk mengatasi persamaan yang kompleks atau tidak dapat menyelesaikan secara analitis.
Metode Biseksi: Metode ini mengandalkan konsep pembagian interval secara berulang untuk mencari nilai X yang memenuhi persamaan. Persamaan harus memiliki tanda berbeda di dua ujung interval yang ditentukan. Dengan membagi interval menjadi setengah, kita dapat menentukan di mana nilai X terletak. Langkah ini diulang hingga akurasi yang diinginkan tercapai.

Metode-metode numerik ini sering digunakan dalam kasus-kasus di mana tidak ada solusi analitis yang sederhana atau persamaan tersebut terlalu rumit untuk diselesaikan secara langsung. Metode numerik memanfaatkan kekuatan komputasi untuk melakukan perhitungan dan pendekatan yang lebih akurat dalam menemukan nilai-nilai X yang memenuhi persamaan.

Dalam beberapa kasus, persamaan dapat memiliki lebih dari satu nilai X yang memenuhi. Terkadang, persamaan memiliki solusi tunggal, sedangkan dalam kasus lain, terdapat solusi ganda atau bahkan tak hingga. Bergantung pada jenis persamaan dan sifat matematika yang terlibat, solusi-solusi ini dapat ditemukan menggunakan metode yang tepat.

kesimpulan

menemukan nilai X yang memenuhi suatu persamaan melibatkan berbagai metode, mulai dari manipulasi sederhana hingga pendekatan numerik yang kompleks. Penting untuk memahami konsep matematika dasar dan memilih metode yang sesuai dengan jenis persamaan yang ada. Dengan pemahaman yang baik dan alat yang tepat, kita dapat menemukan solusi yang akurat dan memenuhi persamaan matematika yang kita hadapi.